Foro de comentarios y dudas. Examen 1
Re: Foro de comentarios y dudas. Examen 1
Re: Foro de comentarios y dudas. Examen 1
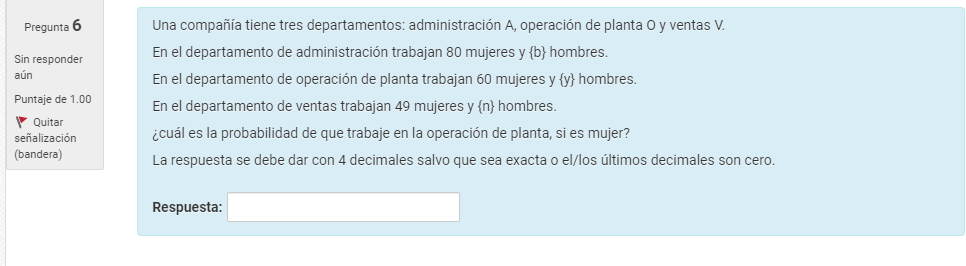
En este problema no aparecen los datos necesarios para contestar a la pregunta.
Re: Foro de comentarios y dudas. Examen 1
Gracias por avisarme Victor, la pregunta se puede contestar con los datos que están, si trato de modificar la pregunta ahora se generan otro conjunto de datos y puede afectar a los que ya contestaron la pregunta.
Re: Foro de comentarios y dudas. Examen 1
Pedí la opción correcta, no las opciones correctas
Re: Foro de comentarios y dudas. Examen 1
Hasta podría poner que la respuesta era 0.00793650793, no es que no supiera responderla, es que no leí bien u_u (y me costó 1.5 puntos)
Pedí 4 decimales a partir del primer decimal distinto de cero, solo pusiste 2
Re: Foro de comentarios y dudas. Examen 1
Re: Foro de comentarios y dudas. Examen 1
Hola
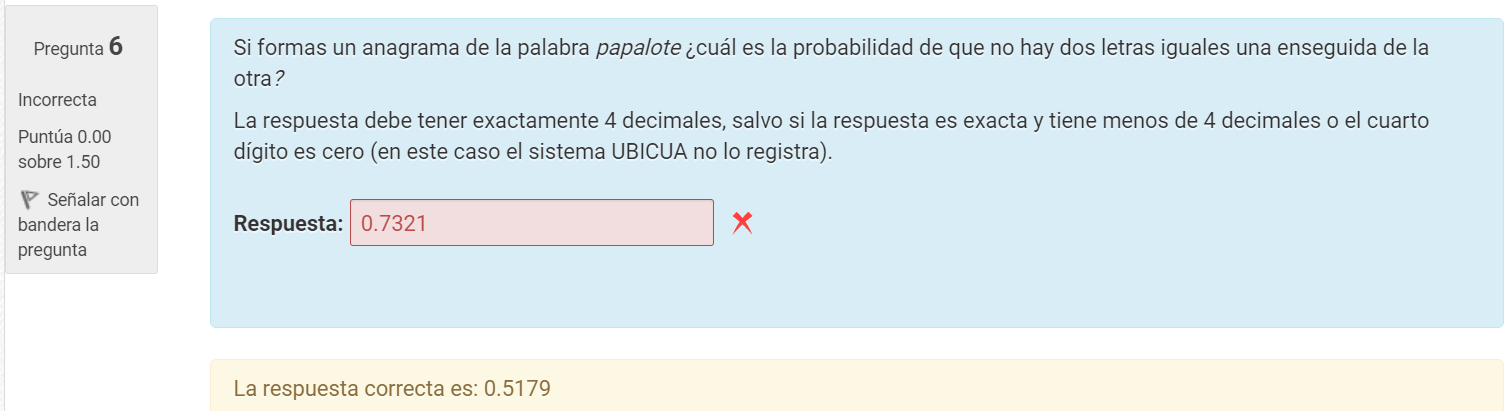
No supe cómo resolver éste problema del examen, ¿podría por favor alguien explicarme?
Re: Foro de comentarios y dudas. Examen 1
x2 jaja, tampoco supe cómo :c
El numero total de anagramas distintas es 8!/2!2!=10080 ya que hay 8 letras en total y hay 2 a's y 2 p's.
Así \(|\Omega|=10080\).
Para contestar el problema, vamos a calcular el numero de anagramas en donde hay al menos dos letras iguales juntos.
Se puede calcular este numero usando el teorema de inclusion exclusion.
Sea \(A\) el conjunto de anagramas en donde las dos a's están juntas y las p' pueden estar juntas o no:
Tienes 7 letras (porque las a's se tomas como una letra al estar juntas) y solo se repite la letra p.
Hay 7!/2! anagramas de este tipo, es decir \(|A|=7!/2!\).
Si \(B\) es el conjunto de anagramas donde las dos p's están juntas y donde las a's pueden estar juntas o no, tenemos análogamente que \(|B|=7!/2!\).
Hay 6! anagramas donde las dos a's están juntas y las dos p's están juntas, es decir \(|A\cap B|=6!\).
Usando el teorema de inclusion exclusion tenemos que \(|A\cup B|=|A|+|B|-|A\cap B|=7!/2+7!/2-6!=4320\).
El número de anagramas donde no hay dos letras iguales una enseguida de la otra es 10080-4320=5760
Por lo que la probabilidad de que no hay dos letras iguales una enseguida de la otra en un anagrama de papalote es 5760/10080=0.5714