Anexo
| Sitio: | Ubicua |
| Curso: | 20-I ÁLGEBRA LINEAL I (CD01MA) |
| Libro: | Anexo |
| Impreso por: | Invitado |
| Fecha: | martes, 30 de diciembre de 2025, 13:15 |
Descripción
ejemplos
1. Independencia lineal
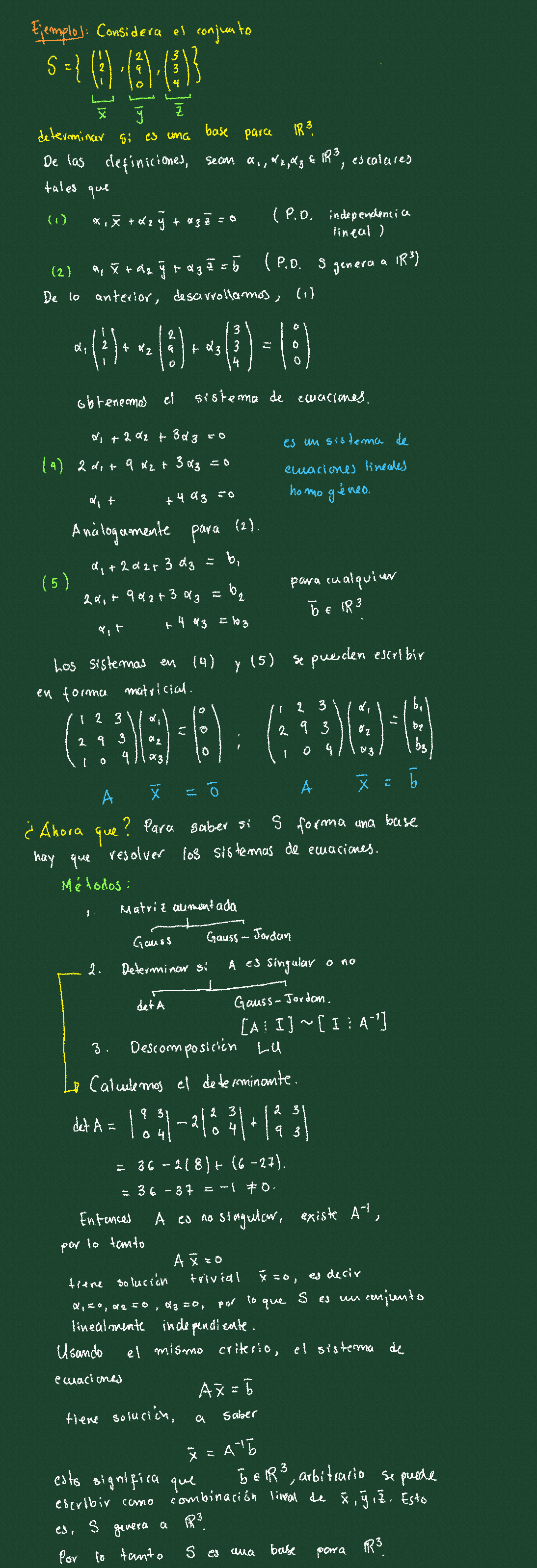
2. Ejemplo 1
Una vez demostrado que el conjutno S forma una base para el espacio tridimensional, podemos graficarlo. Con estos nuevos vectores, se pueden "dibujar" todos los demás que se encuentran en \(\mathbb{R}^3\). Es decir, tenemos un nuevo sistema de coordenadas.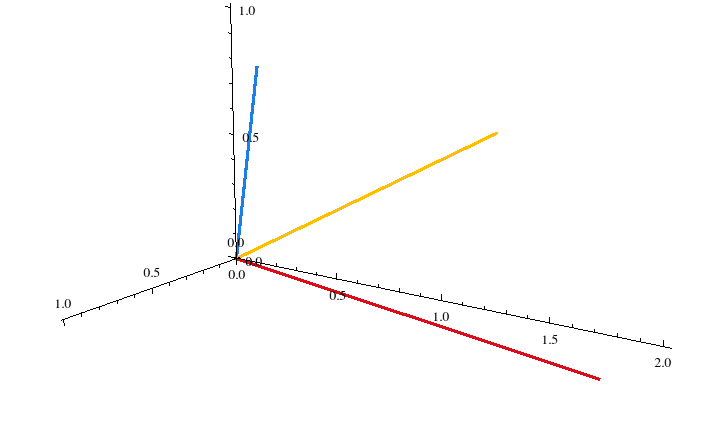
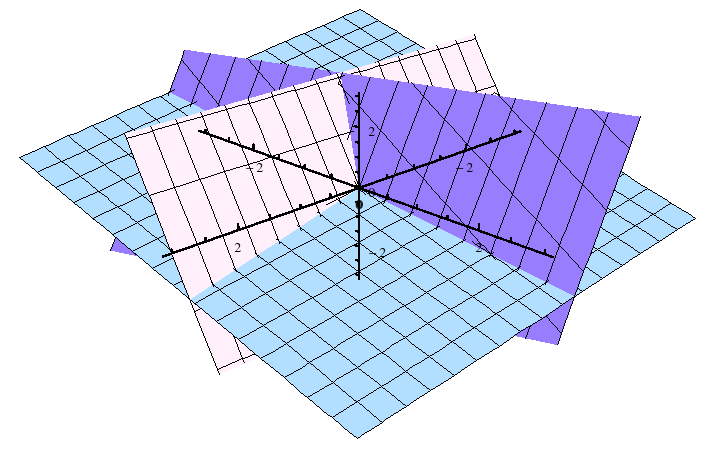
3. PLANOS!
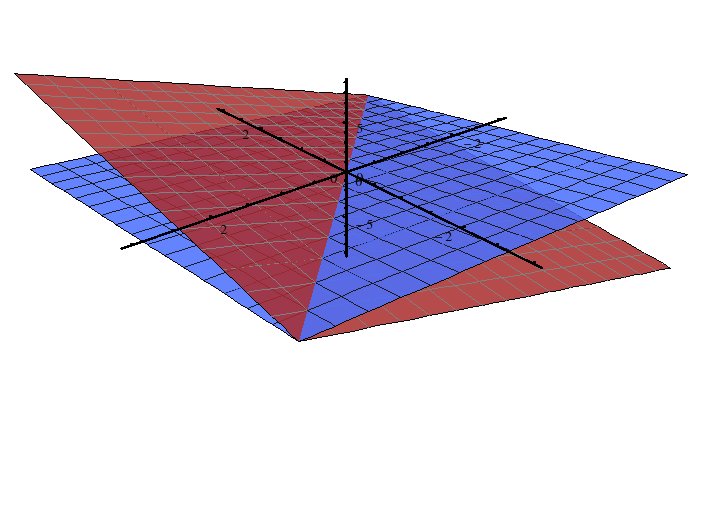
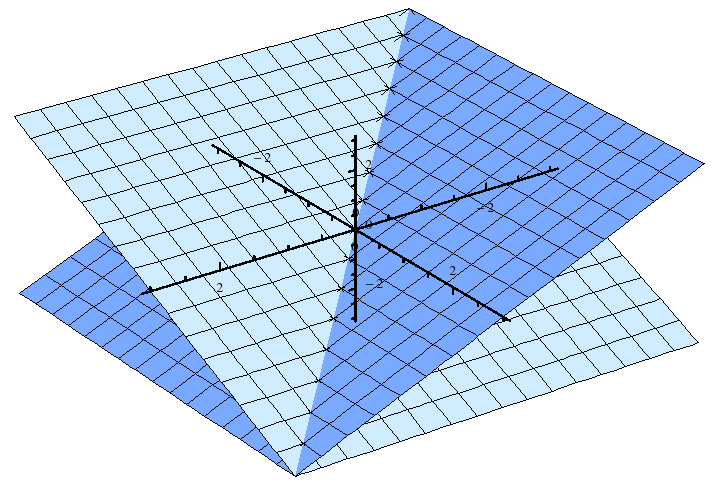
El sistema de ecuaciones (1). Se puede interpretar como las ecuaciones de tres planos que pasan por el origen. La solución del sistema de ecuaciones representa aquellos puntos que pertenecen a los tres plano. Como se demostró, el único punto que satisface las tres ecuaciones de los planos es el vector (0,0,0)
4. Dependencia lineal

5. Solución Geométrica
Tomando las ecuaciones del ejemplo 2.
x+y=0
x+z=0
-y+z=0
Donde las ecuaciones 1 y 2 pueden escribirse como una sola. Entonces tenemos un sistema de dos ecuaciones con dos incógnitas.
Al resolver el sistema se obtuvo una solución paramétrica v=(-y,y,y), es decir, la intersección de dos planos da como solución una recta.
6. Polinomios

7. Otro Ejemplo

8. Otra perspectiva
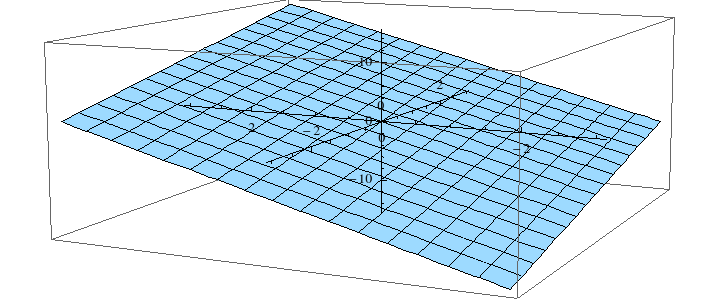
En el ejemplo anterior, el conjunto S es la colección de puntos en el espacio tales que satisfacen la ecuación del plano
2x-y+3z=0. Este plano tiene vector normal
n=(2,-1,3),
que son los coeficientes de la ecuación y se obtiene haciendo el producto vectorial entre (1,2,0) y (0,3,1) que son los elementos de la base. Nótese que S es de dimensión 2, ¡obvio, es un plano!
9. Otra Base
-

-