Geometría del plano y el espacio (revisited)
| Sitio: | Ubicua |
| Curso: | 20-I ÁLGEBRA LINEAL I (CD01MA) |
| Libro: | Geometría del plano y el espacio (revisited) |
| Impreso por: | Invitado |
| Fecha: | lunes, 29 de diciembre de 2025, 04:54 |
Descripción

1. Introducción
En esta sección repasaremos los elementos de la geometría vectorial en \(\mathbb{R}^2\) y \(\mathbb{R}^3\), es decir, definiciones y las operaciones básicas, así como resulados importantes sobre vectores que se usarán a lo largo del curso. Cabe mencionar que Álgebra a Lineal no solo son vectores en el espacio euclidiano, esta disciplina va más allá de un sistema coordenado.

2. Elementos del espacio
CANTIDAD ESCALAR: Definida por un número real, representa una magnitud.
Ejemplos: área, longitud, volumen, masa, temperatura.
CANTIDAD VECTORIAL: Definida cuando se especifica una magnitud y una dirección.
Ejemplos: velocidad, fuerza, desplazamiento.
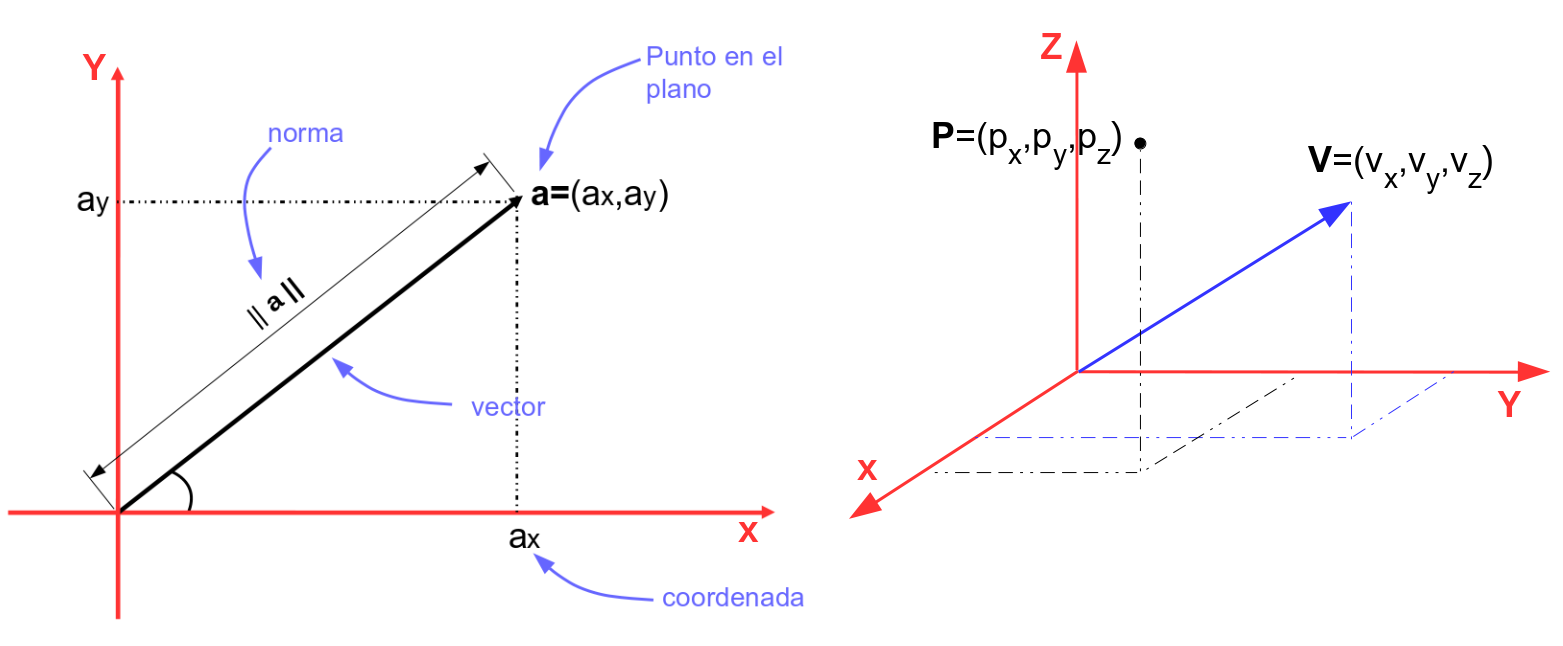
Observación: En algunas literaturas se puede encontrar que un vector queda definido cuando se determina su magnitud, dirección y sentido. Sin embargo, la dirección y el sentido se puede entender como uno mismo cuando se considera la dirección como significado del la recta que contiene al vector en cuestión, el cual toma el mismo sentido en que se ha definido la recta.
3. Notación
Para representar vectores suelen emplearse letras en negritas o con superflechas, es decir:
a, b, X, Y, V, \(\large \overrightarrow{a}\),\(\overrightarrow{b}\), \(\overrightarrow{X}\), \(\overrightarrow{Y}\), \(\overrightarrow{V}\).
Si \(P\) y \(Q\) representan puntos en el espacio, entonces el segmento dirigido que va de \(P\) a \(Q\) se puede escribir como:
\(\bf{v}=\overline{\mathrm{\it PQ}}=\overrightarrow{PQ}\).
Los vectores en \(\mathbb{R}^2\) y \(\mathbb{R}^3\) se pueden escribir como pares ordenados o ternas ordenadas, respectivamente, esto es
\({\bf x}=(x_1,x_2) \), \({\bf y}=(y_1,y_2,y_3) \).
Donde cada coordenada puede ser un número: \(\large \mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}, \mathbb{C}\), o bien otro tipo de objeto.
Nota: En muchos ejemplos que aparecen en los libros, los vectores suelen tener coordenadas enteras, por facilidad operacional y regla didáctica.
4. Operaciones Básicas
La estructura algebráica de los vectores incluye dos operaciones básicas suma y producto por escalares.
Suma
Si \({\bf A},{\bf B}\) son vectores, entonces \({\bf A}+{\bf B}\) es un nuevo vector resultado de la suma de los anteriores.
Producto por escalares
Si \({\bf A}\) es un vector y \(\alpha\) es un escalar, entonces \(\alpha {\bf A}\) es el vector resultante de multiplicar las cantidades dadas.
Las operaciones anteriores satisfacen las siguientes propiedades
Conmutatividad
Dados los vectores \({\bf A}, {\bf B}\) entonces \({\bf A}+ {\bf B}={\bf B}+{\bf A}\).
Asociatividad sobre la suma
Dados los vectores \({\bf A}, {\bf B}, {\bf C}\) entonces \(({\bf A}+ {\bf B})+{\bf C}={\bf A}+({\bf B}+{\bf C}\).
Inverso aditivo
Para cada\({\bf A}\) y el escalar \(\alpha=-1\), se tiene que \(\alpha{\bf A}=-{\bf A}\) es tal que \({\bf A}+ {-\bf A}={\bf 0}\). Donde el cero es una cantidad vectorial.
Neutro aditivo
Para todo\({\bf A}\) vector, existe un vector \({\bf 0}\), llamado vector nulo o vector cero, es tal que \({\bf A}+ {\bf 0}={\bf A}\). Donde este vector tiene magnitud nula y cualquier dirección.
Asociatividad sobre el producto de escalares
Dados los escalares \(\alpha.\beta\) y el vector \({\bf A}\) entonces \(\alpha(\beta{\bf A})=(\alpha\beta){\bf A}\).
Distributividad
Dados \({\bf A}, {\bf B}\) y \(\alpha\) entonces \(\alpha({\bf A}+ {\bf B})=\alpha{\bf A}+ \alpha{\bf B}\). De manera similar, dados \(\alpha, \beta\) y \({\bf A}\) entonces \((\alpha+\beta) {\bf A }= \alpha{\bf A}+\beta {\bf A}\).
Posteriormente los vectores serán tratados como esos objetos abstractos que son elementos de un espacio vectorial, así como se vió en la noción de conjunto.
5. Ejemplos
En el siguiente documento te comparto unos ejemplos

6. Ejemplos

7. Ejemplos

8. Ejemplos
